树结构——层序遍历

层序遍历，是将每个结点按照深度归类进行遍历输出。
层序遍历优点：

能解决最短/最少结点问题，探索深度小。
每个结点只访问一次。
缺点：
内存消耗较大

思路

层序遍历的顺序是，分别遍历每个深度的结点。
示例：

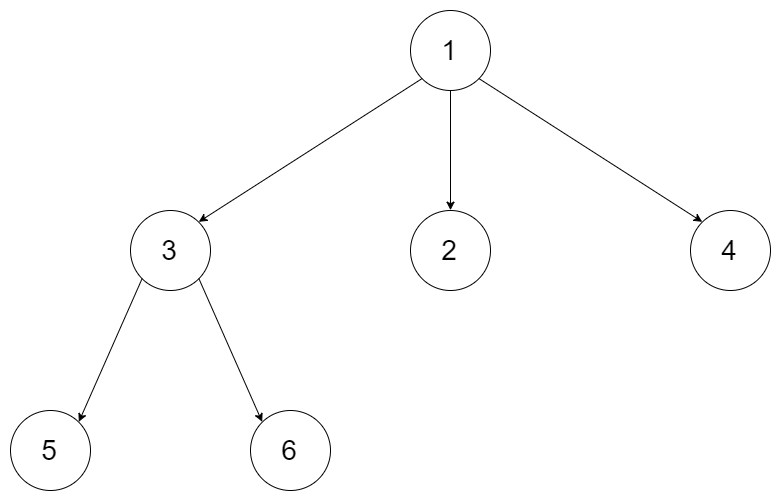
结果:[[1],[3,2,4],[5,6]]

代码

前提：

//结点结构
public class Node {
    public int val;
    public IList<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, IList<Node> _children) {
        val = _val;
        children = _children;
    }
}

// 接收的入口
public IList<IList<int>> LevelOrder(Node root) {
    IList<IList<int>> list = new List<IList<int>>();
    if(root == null){
        return list;
    }

    InOrder(root,list);
    return list;
}

迭代法

迭代方案来处理一般比递归要简单一点。

使用队列前进先出的特点，可以保证是层序的遍历顺序。不过难点在于输出要每个深度一个分组的结果，那么如何得知当前结点是什么深度就很重要。

如果提供的树结构没有depth的字段，那么只能通过计数方式来获取。可以想象队列中的顺序就是层序顺序，所以只要知道第几个结点出队列时表示该深度遍历结束即可。

那么就需要两个参数来做记录。nodeCount 和 childCount 。

nodeCount记录的是本深度的结点数量，每次出队列时该参数-1。当nodeCount == 0时，表示该层的全部都出队列了，那么接下来该是下一深度的计数。而下一深度的结点数量刚好可以通过childCount来获得。
childeCount记录每次子节点的遍历数量，当childCount被赋值给nodeCount时，表示当前层结点遍历完毕，childCount已经记录了下一层的所有结点数量。接着进行下一层之前赋值为0，就继续计数下下一层的节点数量。


private void InOrder(Node node,IList<IList<int>> list){
    // 层序遍历是，从上到下，从左到右, 每层是一个序列。
    // 这一般要使用队列来实现。先遍历同层结点，先出的就是父节点后出的就是子节点了。
    // 问题是，怎么确认一层的结束呢，计数

    if(node == null){
        return;
    }

    Queue<Node> queue = new Queue<Node>();
    queue.Enqueue(node);
    int nodeCount = 1;  // 当为0时，表示该层结束，获取childCount继续计时
    int childCount = 0; // 在nodeCount 为0之前，每次child入队列都累计计数，将数值交给nodeCount时，才归0
    int depth = 1;  // nodeCount归0时，深度就会增加

    while(queue.Count > 0){
        Node pNode = queue.Dequeue();
        nodeCount --;

        IList<int> cellList = null;
        if(depth > list.Count){ // 深度大于结果数，表示没有创建
            cellList = new List<int>();
            list.Add(cellList);
        }else{
            cellList = list[depth-1];
        }
        cellList.Add(pNode.val);

        // 接着子结点入队列
        if(pNode.children != null && pNode.children.Count > 0){
            for(int i = 0; i < pNode.children.Count;i++){
                queue.Enqueue(pNode.children[i]);
            }

            childCount += pNode.children.Count;
        }

        // 接着处理计数
        if(nodeCount == 0){
            // nodeCount == 0 表示当前depth 已经遍历完成
            // childCount 此时获取到的是下一层的子节点总数
            nodeCount = childCount;
            childCount = 0; // 重新计数
            depth++; // 层数增加，接下来是下一层的工作
        }

    }
}

其中的depth我用参数来记录，不过仅仅为了解决问题，其实可以直接使用list.Count 来代替depth，其主要作用就是取出当前深度的结果数组，将结果加入到当前结果数组中。

递归法（不建议）

递归方案能看出来和深度搜索中前序遍历很像。

所以这个只是结果为层序，但遍历顺序并不是。

关键仅仅是传递了depth，将结果提供给指定depth的数列中。

！！层序遍历不要使用此方法，此方法仅仅是让结果正确而已。其实质依旧是前序遍历！！

// 注：方法传递提供depth参数，所以调用时起始传递depth = 1
// InOrder(root,list,1);

    private void InOrder(Node node,IList<IList<int>> list,int depth){
        // 层序遍历是，从上到下，从左到右, 每层是一个序列。
        // 递归写法,传递depth 可以将结果直接输出到正确的深度结果中
        IList<int> res = null;
        if(depth > list.Count){
            res = new List<int>();
            list.Add(res);
        }else{
            res = list[depth-1];
        }

        res.Add(node.val);

        // 子节点递归
        if(node.children != null && node.children.Count > 0){
            for(int i = 0; i < node.children.Count;i++){
                InOrder(node.children[i],list,depth + 1);
            }
        }
    
    }

CrabSaberV is here

树-层序遍历(广度优先搜索)

树结构——层序遍历

思路

代码

迭代法

递归法（不建议）