树-后序遍历

树结构的深度遍历-前序遍历

树结构的深度遍历，本次介绍的是后序遍历方法。

介绍

后续遍历其实和前序遍历思路基本一致，唯一不同的是遍历路径是：子节点->父节点。

示例：

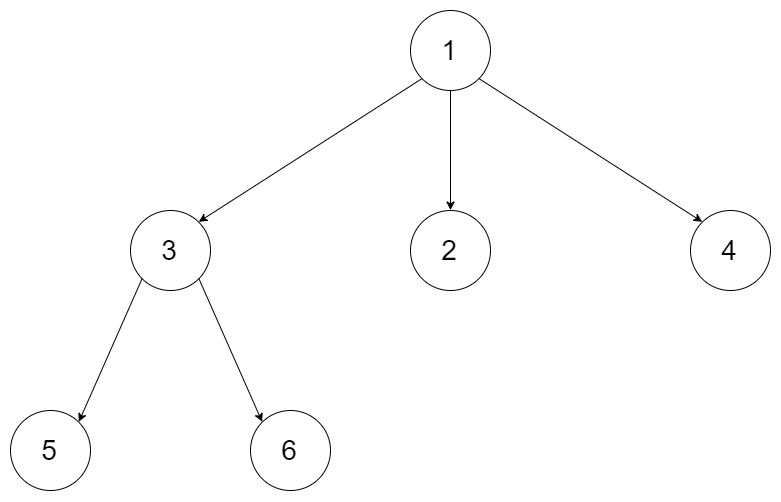
结果：[5,6,3,2,4,1]

代码

代码前提：

// 结点结构
public class Node {
    public int val;
    public IList<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,IList<Node> _children) {
        val = _val;
        children = _children;
    }
}

// 调用接口
public IList<int> Postorder(Node root) {
    IList<int> list = new List<int>();
    if(root == null){
        return list;
    }

    InOrder(root,list);
    return list;
}

递归方案

private void InOrder(Node node,IList<int> list){
    // 后续遍历，是先遍历子节点，再遍历父节点
    // 递归法

    if(node == null){ // 递归结束条件很重要
        return;
    }

    // 先是子节点，子节点结束后就是父节点
    if(node.children != null && node.children.Count > 0){
        for(int i = 0; i < node.children.Count; i++){
            InOrder(node.children[i],list);
        }
    }
    list.Add(node.val);   
}

迭代方案(1)

此迭代方案是模拟递归方式实现。
不过由于需要先遍历子节点，子节点结束后会再一次访问父节点，结点存在遍历两次的情况，所以需要一个数组记录已经遍历过子节点的结点。

这样如果结点已经遍历过子节点，那么就可以直接放心输出了。

private void InOrder(Node node,IList<int> list){
    // 后续遍历，是先遍历子节点，再遍历父节点
    // 迭代法，参考递归的方案，先深层遍历子节点，后再输出父节点

    if(node == null){ // 递归结束条件很重要
        return;
    }
    // 需要一个记录结点是否遍历过子节点的集合
    IList<Node> overNodes = new List<Node>();
    Stack<Node> stack = new Stack<Node>();
    stack.Push(node);

    while(stack.Count > 0){
        
    Node pNode = stack.Peek(); // 看探查

    // 如果结点到头，或者已经输出过子节点了，那么出栈且输出
    if(pNode.children == null || pNode.children.Count <= 0 || overNodes.Contains(pNode)){
        stack.Pop();
        list.Add(pNode.val);
        continue;
    }

    // 先将子节点都遍历了
    if(pNode.children != null && pNode.children.Count > 0){
        for(int i = pNode.children.Count - 1; i >= 0; i--){
            stack.Push(pNode.children[i]);
        }
    }
    // 标记该结点已经遍历过子节点了
    overNodes.Add(pNode);
}

迭代方案(2)

该方法比较简单，后续遍历的结果其实与前序遍历相反，所以先按照前序遍历进行一次遍历，然后结果反转即可。

需要注意本次的前序遍历中，子节点的出栈顺序就必须是反序的了。

private void InOrder(Node node,IList<int> list){
    // 后续遍历，是先遍历子节点，再遍历父节点
    // 迭代法，先前序，后反转结果。
    // 需要注意的就是前序的子节点遍历时要与前序的结果相反。

    if(node == null){ // 递归结束条件很重要
        return;
    }
    // 需要一个记录结点是否遍历过子节点的集合
    Stack<Node> stack = new Stack<Node>();
    stack.Push(node);

    while(stack.Count > 0){ 
            
        Node pNode = stack.Pop(); 
        // 输出
        list.Add(pNode.val);

        // 先将子节点都遍历了
        if(pNode.children != null && pNode.children.Count > 0){
            for(int i = 0; i < pNode.children.Count; i++){
                stack.Push(pNode.children[i]);
            }
        }
            
    }

    ((List<int>)list).Reverse(); // 转为List，再反转结果
       
}

该方案简单，而且性能也比较好，比较推荐这种写法。