树-前序遍历

树结构的深度遍历-前序遍历

树结构的深度遍历，本次介绍的是前序遍历方法。

介绍

其实了解了深度遍历的思想，前序遍历很简单，仅仅是结点的遍历顺序问题而已。

前序遍历是按照深度遍历的路径，优先遍历父节点的方案进行遍历。

顺序可以简单理解为：父节点->子节点（左到右）

看下图的例子

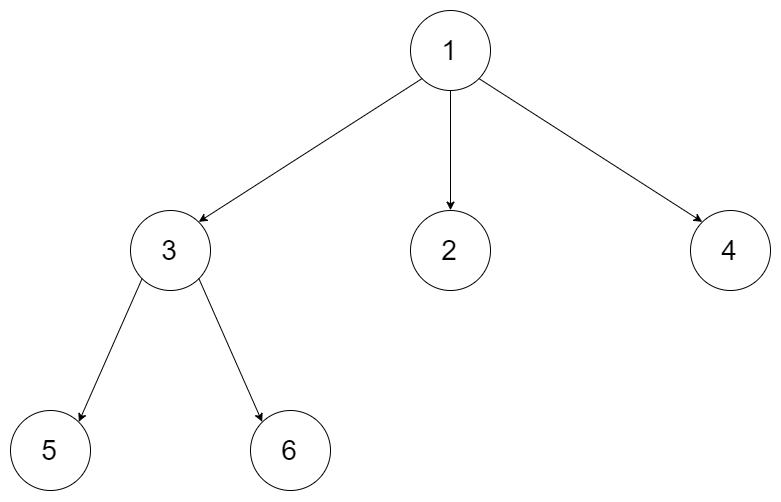
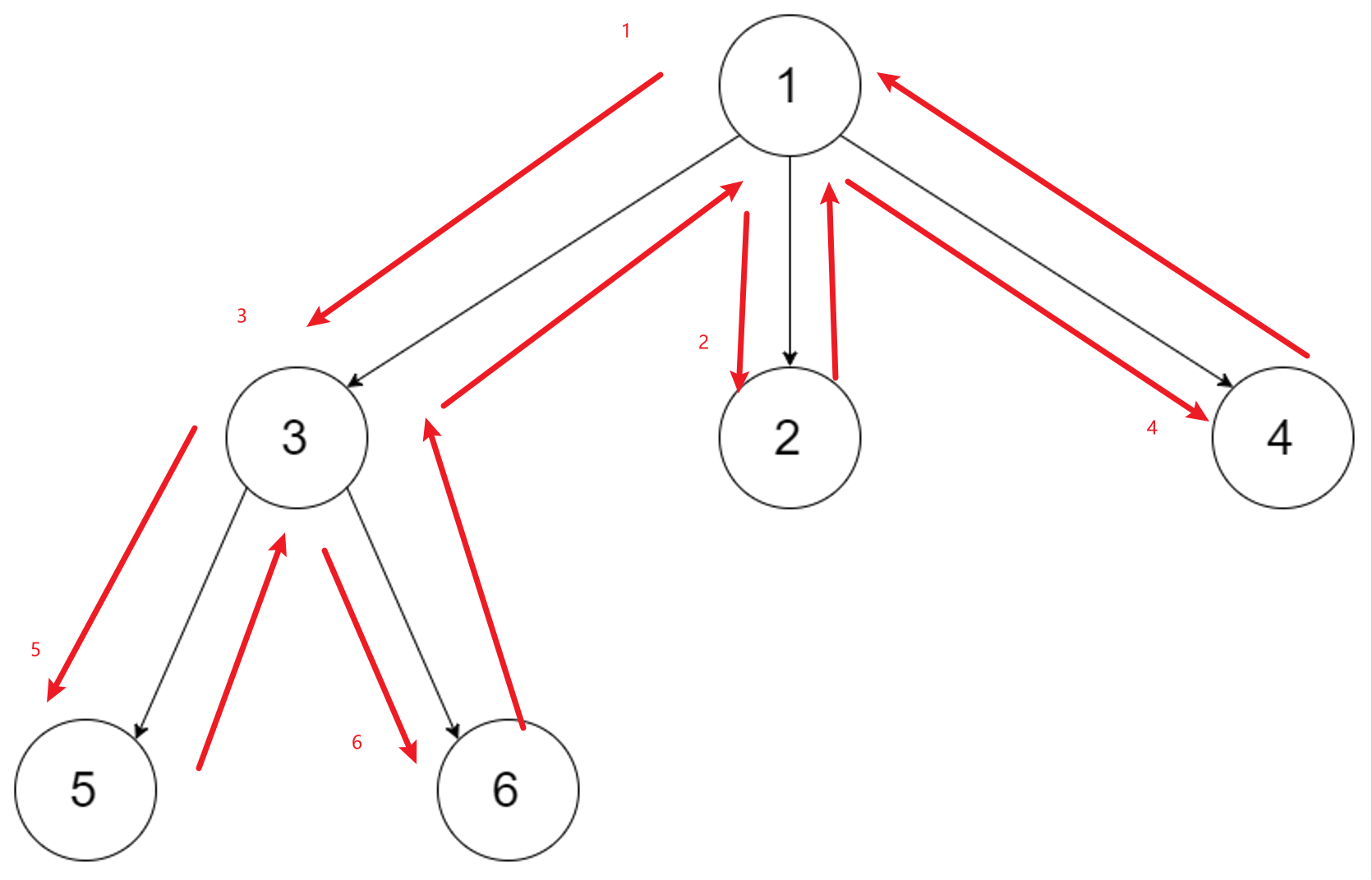
前序遍历结果为：[1,3,5,6,2,4] 其过程为下图

代码

代码前提：

// 结点结构
public class Node {
    public int val;
    public IList<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,IList<Node> _children) {
        val = _val;
        children = _children;
    }
}

递归方法

public IList<int> Postorder(Node root) {
    IList<int> list = new List<int>();
    if(root == null){
        return list;
    }

    InOrder(root,list);
    return list;
}

// 遍历方法
private void InOrder(Node node,IList<int> list){
    // 前序遍历，是先遍历父结点，然后是子节点
    if(node == null){ // 递归结束条件很重要
        return;
    }

    list.Add(node.val);
    // 后是子节点
    if(node.children != null && node.children.Count > 0){
        for(int i = 0; i < node.children.Count; i++){
            InOrder(node.children[i],list);
        }
    }

}

迭代方案

public IList<int> Preorder(Node root) {
    // 前序遍历，就是先遇到哪个结点就将其输出，从上到下，从左到右
    // 迭代的写法
    IList<int> list = new List<int>();
    if(root == null){
        return list;
    }

    Stack<Node> stack= new Stack<Node>();
    stack.Push(root); // 先从根结点开始

    while(stack.Count > 0){
        Node node = stack.Pop();
        list.Add(node.val);
        if(node.children != null && node.children.Count > 0){
            // 因为子节点顺序是从左往右遍历的，所以入栈时要反着入栈
            for(int i = node.children.Count - 1; i >= 0;i--){
                stack.Push(node.children[i]);
            }
        }
    }

    return list;

}