二叉树——中序遍历

为什么这里特指二叉树的中序遍历呢？因为中序遍历的顺序是：左子结点->父结点->右子结点，如果是N叉树就不符合这个顺序特征了。

思路

按照左子结点->父结点->右子结点的顺序遍历即可。如果是递归法，那么控制递归顺序就能实现。

下图例子：

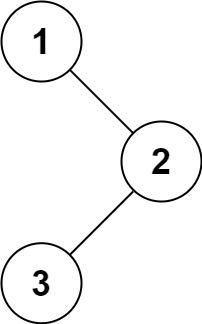
结果为:[1,3,2]

代码

前提代码

public class TreeNode {
     public int val;
     public TreeNode left;
     public TreeNode right;
     public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
}

public IList<int> InorderTraversal(TreeNode root) {
    // 只有二叉树有中序遍历
    // 其逻辑是，遍历顺序是：左子节点 -> 父节点 -> 右结点
    IList<int> list = new List<int>();
    if(root == null){
        return list;
    }

    InOrder(root,list);

    return list;
}

递归法

private void InOrder(TreeNode node,IList<int> list){
    if(node == null){
        return;
    }

    InOrder(node.left,list);
    list.Add(node.val);
    InOrder(node.right,list); 
}

迭代法

这里迭代法我写两个方案，一份是我自己的思路，一份是官方给的思路。
我自己的思路虽然解决了问题，但额外引入了数组，代码稍显笨拙。
官方的思路代码比较简单。

迭代法1（个人）

按照中序的路径：左子节点->父节点->右子结点，那么入栈顺序要保证：右子节点->父节点->左子节点。
其中特别点是一个树杈的“左子节点->父节点->右子结点”都是紧挨在一起在栈内的。

遍历时先考虑将右子节点入栈。条件是右子节点没有在栈内，同时也没有输出过。（因为当父节点出栈时,走循环内的流程，要防止重复将右结点入栈）
如果左子结点存在，且没有输出过，那么继续深入遍历，就需要将当前结点和左子节点入栈;
如果左子结点不存在，或者左子节点已经被输出过了，那么可以说明现在处于回溯的流程中，就可以输出该结点了，同时将该结点存储到已输出序列中。
按照上述逻辑，直到栈空则遍历完毕了。

private void InOrder(TreeNode node,IList<int> list){
    if(node == null){
        return;
    }

    List<TreeNode> overNodes = new List<TreeNode>(); // 记录输出过的node
    Stack<TreeNode> stack = new Stack<TreeNode>();
    stack.Push(node);

    while(stack.Count > 0){
        TreeNode pNode = stack.Pop();

        // 确保栈中没有，且没有被输出过才入栈
        if(pNode.right != null && !overNodes.Contains(pNode.right) && (stack.Count <= 0 || stack.Peek() != pNode.right)){
                // right 不为空，且没被输出，则入栈
            stack.Push(pNode.right);
        }
        if(pNode.left == null || overNodes.Contains(pNode.left)){
            // left 已经输出过了，则打印该node
            list.Add(pNode.val);
            overNodes.Add(pNode);
        }else{
            // 有 left,且没有打印
            stack.Push(pNode);
            stack.Push(pNode.left);

        }
            
    }
}

缺点：

代码的结点可能有2次入栈遍历，所以事件复杂度为O(logn)
引入了一个数组用于记录输出的结点，增加了空间和时间。

迭代法1（官方）

其步骤是：

每次循环，先内部循环将结点下的左节点入栈，直到为空。（因为深入遍历过程中，父节点和左子节点是同一个方向）
当内部遍历左结点结束后，出栈一个结点就可以输出。
接着入栈一个右节点，来对右节点进行同样的内部循环遍历过程。

能看出来也是递归方案的迭代写法，而且看着很清晰。迭代写法中每次迭代都是先深入左子节点，然后回溯到父节点，接着是由结点做同样操作。

private void InOrder(TreeNode node,IList<int> list){
    if(node == null){
        return;
    }

    Stack<TreeNode> stack = new Stack<TreeNode>();
    while (node != null || stack.Count > 0) {
        while (node != null) {
            stack.Push(node);
            node = node.left;
        }
        node = stack.Pop();
        list.Add(node.val);
        node = node.right;
    }
 
}

我写出来的代码较为臃肿，也说明我对递归到迭代的理解还不够透彻。

CrabSaberV is here

树-中序遍历

二叉树——中序遍历

思路

代码

递归法

迭代法

迭代法1（个人）

迭代法1（官方）