前言
计算机起初是为进行科学计算而设计的,也就是服务于数学
回顾一下高数的知识—-向量
向量点乘(内积)
公式
对于向量a和向量b
- a = [a1,a2,a3…an]
- b = [b1,b2,b3..bn]
a • b = a1b1 + a2b2 + a3b3 + … + anbn
(注意:a与 b 长度要相同)
意义
点乘的几何意义一般用于计算或表示两个向量的夹角,以及b在a上的投影。
公式:
a • b = |a||b|cos θ
叉乘
两个向量的叉乘,又叫向量积、外积、叉积、叉乘。
向量叉乘的结构往往与两向量构成的平面垂直。
公式
a = (x1,y1,z1)
b = (x2,y2,z2)
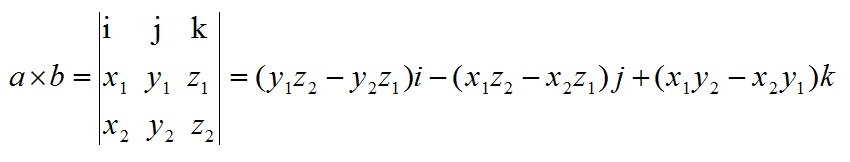
- i = (1,0,0) j = (0,1,0) k = (0,0,1)
意义
在三维几何中,向量a和向量b的叉乘结果也是一个向量,也叫法向量。
法向量垂直于向量a与向量b构成的平面。
向量归一化
向量归一化法有两种形式:
一种是把数变为(0,1)之间的小数
一种是把有量纲表达式变为无量纲表达式。
主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速,应该归到数字信号处理范畴之内。
简单例子
把数变为(0,1)之间的小数
例1:{2.5 3.5 0.5 1.5}归一化后变成了{0.3125 0.4375 0.0625 0.1875}
解:2.5+3.5+0.5+1.5=8,
2.5/8=0.3125,
3.5/8=0.4375,
0.5/8=0.0625,
1.5/8=0.1875
这个归一化就是将括号里面的总和变成1,然后写出每个数的比例。